排列组合是数学中一个重要的基本概念，它包括排列和组合两个部分。排列是指从n个不同元素中取出m个元素进行排序的数学方法，其基本公式为P(n,m)=n!/(n-m)!；组合则是指从n个不同元素中取出m个元素不考虑顺序的数学方法，其基本公式为C(n,m)=n!/[m!(n-m)!]。排列组合不仅在数学、物理、计算机科学等领域有广泛应用，还与日常生活中的许多问题密切相关，如安排日程、选择队伍等。掌握排列组合的基本公式，就如同拥有了一把解锁数学世界奇妙之门的钥匙，能够让我们更加深入地理解和应用这些概念，解决更复杂的问题。

在数学的广阔天地中，排列组合作为离散数学的一个重要分支，不仅在理论研究中占据一席之地，更在日常生活、计算机科学、统计学等多个领域中发挥着不可替代的作用，它像一把神奇的钥匙，为我们打开了理解复杂问题、优化资源配置、设计实验方案等众多难题的大门，本文将深入浅出地介绍排列组合的基本概念、重要性以及两大核心公式——排列公式和组合公式的应用与理解。

一、排列组合的初探：从日常到抽象

排列（Permutation）与组合（Combination）看似简单，实则蕴含着深奥的逻辑与数学之美，排列是指从n个不同元素中取出m（m≤n）个元素，按照一定的顺序进行排列的过程；而组合则是指从n个不同元素中取出m个元素，不考虑顺序的组合方式。

生活实例：假设你计划一场家庭聚会，需要安排5位朋友的座位顺序（排列），但同时你也在考虑邀请哪些朋友参加（组合），并不关心他们坐在哪里。

二、排列组合的数学语言

在数学表达中，排列通常用符号“P”表示，具体为P(n, m) = n! / (n-m)!，!”代表阶乘，即n! = n × (n-1) × ... × 2 × 1，组合则用符号“C”表示，具体为C(n, m) = n! / [m! × (n-m)!]，这两个公式是排列组合理论的核心，它们以简洁的形式概括了从大量元素中选取特定数量元素的所有可能方式。

三、排列公式的深入解析

定义：P(n, m)表示从n个不同元素中取出m个元素进行排列的方法数。

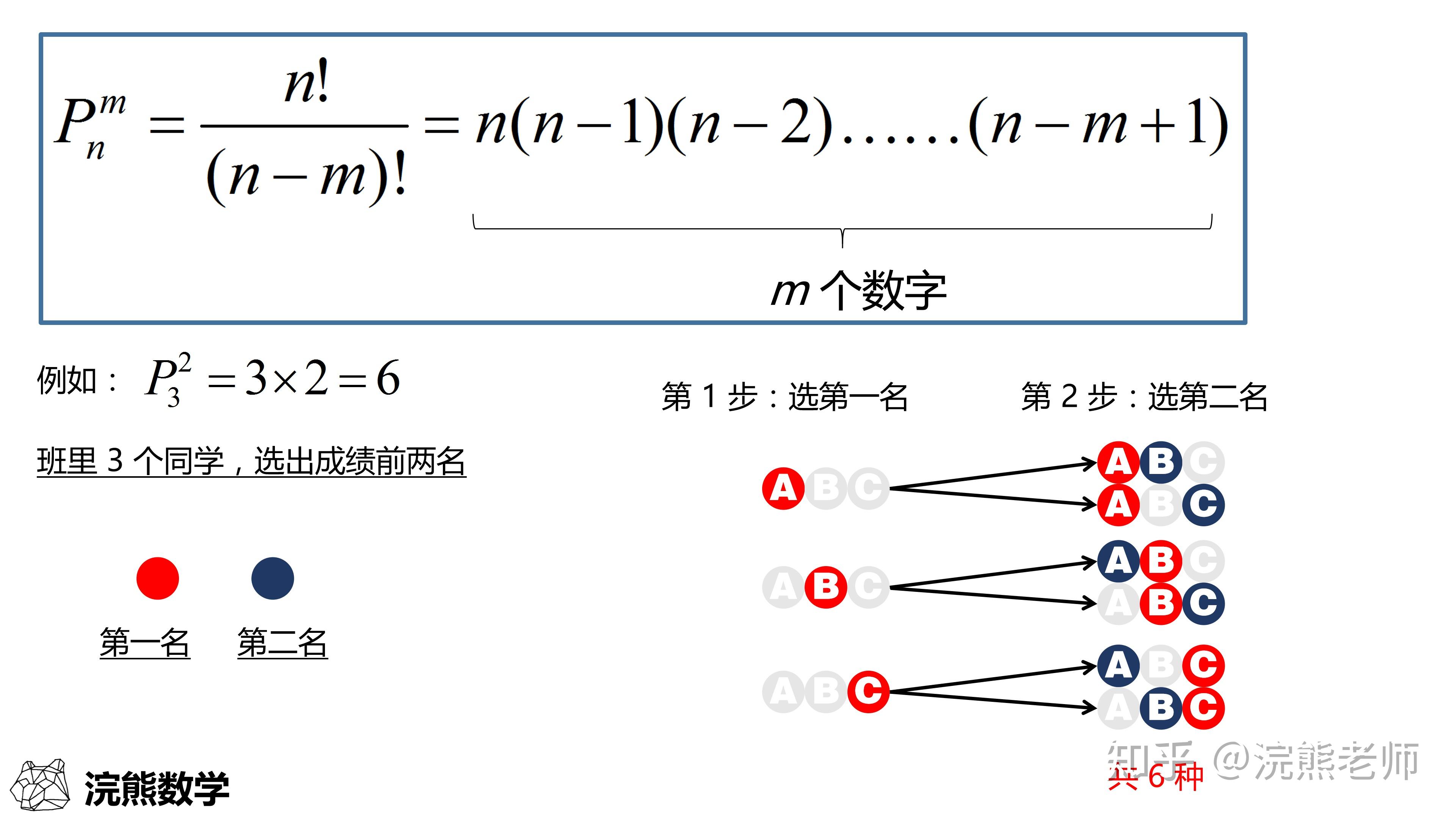
理解：想象有n个不同的球，我们需要从中选出m个球来排成一列，第一个位置有n种选择，第二个位置有剩下的n-1种选择，以此类推，直到最后一个位置，总的排列方式就是n×(n-1)×...×(n-m+1)，即n!/(n-m)!。

例子：从4个不同的字母（A, B, C, D）中选取3个进行排列，共有P(4, 3) = 4! / (4-3)! = 24种不同的排列方式。

四、组合公式的精妙之处

定义：C(n, m)表示从n个不同元素中取出m个元素进行组合的方法数。

理解：与排列不同，组合不考虑顺序，还是以选球为例，如果我们只是想知道能选出多少组包含3个球的不同组合，那么ABD和BDA被视为同一种组合，我们需要用C(n, m)来计算，它通过除以m!来消除重复的顺序效应。

例子：从4个不同的字母中选取3个进行组合，共有C(4, 3) = 4! / [3! × (4-3)!] = 4种不同的组合方式。

五、排列组合的应用领域

1、计算机科学：在算法设计中，排列组合帮助优化搜索路径、设计测试用例等，全排列算法用于生成所有可能的序列来找到最优解。

2、统计学与概率论：在概率计算中，组合用于计算事件的不同发生方式；而排列则用于考虑事件发生的顺序，在计算彩票中奖概率时，需要考虑号码的排列方式。

3、日常生活决策：在安排日程、选择团队成员、设计实验方案时，排列组合原理帮助我们评估所有可能的选项并做出最优选择。

4、密码学与信息安全：在密码学中，排列组合用于生成密钥空间的大小估计，确保密码系统的安全性。

六、排列组合公式的拓展应用与进阶理解

除了基本的P(n, m)和C(n, m)，数学家们还发展了更多高级的排列组合技巧和公式，如包含重复元素的排列（P_r）、包含重复元素的组合（C_r）、带权重的排列与组合等，这些进阶概念在解决特定问题时提供了更强大的工具。

P_r（带重复的排列）：考虑元素可以重复的情况下的排列数计算，从3个不同的球（红、蓝、绿）中取2个进行“带重复”的排列（如RR, BB被视为有效），计算方法需特别处理重复情况。

C_r（带重复的组合）：同样地，当元素可以重复选取时计算组合数的方法也不同于C(n, m)，这通常涉及到更复杂的数学处理或使用特定的公式来避免重复计数。

七、学习排列组合的挑战与建议

学习排列组合时，学生常面临的挑战包括理解抽象概念、记忆复杂的公式以及解决实际问题时的思维转换，为了克服这些挑战：

1、动手实践：通过实际案例和练习题加深理解，如使用小物件进行排列组合的物理演示。

2、图形辅助：利用图形化工具（如树状图、Venn图）帮助理解复杂的排列组合问题。

3、理论联系实际：将抽象的公式与现实生活场景相结合，如安排日程表、设计实验等，使学习过程更加生动有趣。

4、反复练习：通过大量练习来熟悉公式的应用和问题的解决步骤，逐步提高解题速度和准确率。

5、寻求帮助与讨论：与同学、老师或在线社区交流讨论，可以获得不同的解题思路和见解，促进深入理解。

探索数学之美

排列组合不仅是数学学科中的基础而重要的内容，更是开启逻辑思维和问题解决能力的一把钥匙，它教会我们如何以数学的眼光看待世界，如何在纷繁复杂中找到规律和秩序，正如爱因斯坦所说：“不要为已知而教数学，要为未知而教。”通过学习排列组合，我们不仅能够解决眼前的难题，更能培养一种面对未知挑战时的勇气和智慧，让我们在数学的海洋中继续探索，发现更多未知的美丽与奇迹吧！